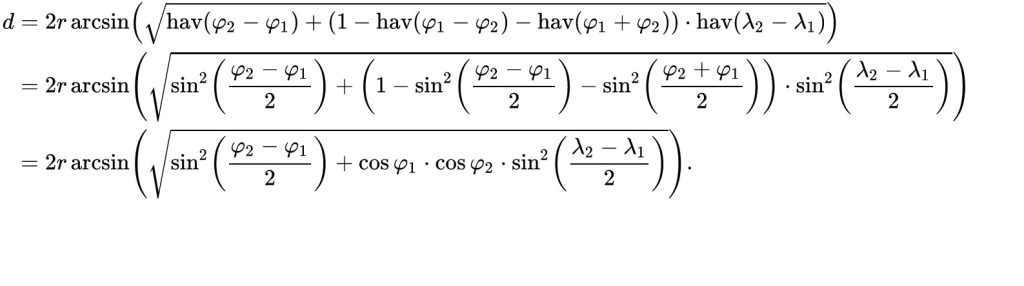The Haversine Formula: Calculating Distances on Earth

The Haversine formula’s historical roots and enduring relevance showcase its unique ability to withstand the test of time. Dating back to the 19th century, this reliable method has proven indispensable in the world of mathematics and geography, providing a means to accurately calculate the great-circle distance between two points on Earth’s surface.

Despite the advent of the digital age, the Haversine formula’s elegant design continues to make it a preferred solution for an array of distance-based calculations, ranging from navigation systems to location-based services.

Delving into the Origins of the Haversine Formula

The Haversine formula is named after the haversine function, a term first introduced by English mathematician James Inman in 1835. Inman’s work focused on determining the distance between two points on a sphere, relying on the haversine function as a core component. The term “haversine” is derived from the combination of the words “half” and “versine,” where the latter refers to a trigonometric function employed in spherical geometry.

The Haversine formula’s development is closely linked to the spherical law of cosines, an integral equation in spherical trigonometry. Although the spherical law of cosines is helpful for calculating distances on a sphere, it often loses accuracy for smaller distances due to rounding errors. In contrast, the Haversine formula offers a more precise solution in such scenarios, rendering it an ideal choice for numerous applications.

The Mathematical Derivation and Practical Applications of the Haversine Formula

The Haversine formula, which is used to calculate the great-circle distance between two points on a sphere with a given radius, is based on the latitude and longitude coordinates of these points. Its mathematical derivation revolves around the use of trigonometric functions like sine and cosine, allowing the formula to account for Earth’s curvature while determining the shortest distance between two points on a sphere.

In the modern world, the Haversine formula’s practical applications span various domains, from navigation and cartography to computer science and data analysis. For instance, the formula is widely used in navigation systems, geographic information systems (GIS), aviation and shipping route optimization, and location-based services. Furthermore, the Haversine formula has emerged as a valuable tool for data analysts and researchers working with geospatial data, enabling them to discern patterns, trends, and correlations involving geographical locations.

In conclusion, the Haversine formula’s rich history and continued relevance demonstrate its enduring efficacy and versatility as a tool for calculating distances on Earth’s surface. Despite its age, the formula remains a mainstay in the realms of mathematics, geography, and technology, underpinning numerous applications that allow us to better understand and navigate our world.

The Origins and Development of the Haversine Formula

The Haversine formula takes its name from the haversine function, a term coined by English mathematician James Inman in 1835. Inman’s work, which focused on calculating the distance between two points on a sphere, relied on the haversine function as a key component. The name “haversine” comes from the combination of “half” and “versine,” where the versine is a trigonometric function used in spherical geometry.

The Haversine formula’s development can be traced back to the spherical law of cosines, a fundamental equation in spherical trigonometry. While the spherical law of cosines is useful for calculating distances on a sphere, it tends to lose accuracy for small distances due to rounding errors. The Haversine formula, on the other hand, offers a more accurate solution in such cases, making it a preferable choice for many applications.

Mathematical Derivation of the Haversine Formula

The Haversine formula calculates the great-circle distance between two points on a sphere with a given radius, using their latitude and longitude coordinates.

The formula is as follows:

a = sin²(difference_in_latitude/2) + cos(latitude1) * cos(latitude2) * sin²(difference_in_longitude/2) c = 2 * atan2(√a, √(1-a)) distance = radius_of_earth * c

To understand the formula, let’s break it down step by step:

1. Convert the latitude and longitude coordinates of both points from degrees to radians.
2. Calculate the differences in latitude and longitude between the two points.
3. Calculate the haversine of the differences in latitude and longitude (a).
4. Compute the angular distance between the two points (c).
5. Multiply the angular distance by the Earth’s radius to obtain the great-circle distance.

By using trigonometric functions like sine and cosine, the Haversine formula effectively calculates the shortest distance between two points on a sphere, taking into account the Earth’s curvature.

Practical Applications of the Haversine Formula

The Haversine formula has found numerous applications in diverse fields, from navigation and cartography to computer science and data analysis. Some of the most common use cases include:

• Navigation Systems: The Haversine formula plays an essential role in modern navigation systems, such as GPS devices and mobile apps, by enabling accurate distance and time estimations between geographical locations.
• Geographic Information Systems (GIS): GIS professionals often rely on the Haversine formula for a wide range of spatial analyses, including proximity calculations, distance-based clustering, and network analyses.
• Aviation and Shipping: In the aviation and shipping industries, the Haversine formula is crucial for calculating optimal flight and shipping routes, taking into account the Earth’s curvature to save time, fuel, and resources.
• Location-based Services: Many web and mobile applications use the Haversine formula to provide location-based services, such as finding the nearest restaurant, calculating travel distances, and estimating arrival times.
• Data Analysis: The Haversine formula is a valuable tool in data analysis, particularly when dealing with geospatial data. Analysts and researchers can employ the formula to examine patterns, trends, and correlations in data sets that involve geographical locations.
• Geocoding and Reverse Geocoding: Geocoding services, which convert addresses into latitude and longitude coordinates, often use the Haversine formula in combination with spatial databases to provide accurate reverse geocoding results (converting coordinates back into addresses).
• Weather Forecasting and Climate Studies: The Haversine formula is a critical component in weather forecasting and climate research, as it helps meteorologists and climatologists assess the spatial distribution of weather patterns and climate-related phenomena.
• Disaster Management and Emergency Response: In disaster management and emergency response planning, the Haversine formula can be used to calculate distances between critical infrastructure, such as hospitals and emergency shelters, and potential disaster zones.

Challenges and Alternatives to the Haversine Formula

While the Haversine formula has proven effective in many situations, it’s essential to consider its limitations. One significant constraint is that the formula assumes a perfect sphere, whereas Earth is more accurately described as an oblate spheroid. For most applications, this simplification yields acceptable results, but for high-precision distance calculations, alternative methods like the Vincenty formula or the ellipsoidal Earth model may be more suitable.

Moreover, the Haversine formula’s reliance on trigonometric functions can lead to potential performance issues when processing large datasets. In such cases, alternatives like the Spherical Law of Cosines or the Equirectangular Projection may offer better computational efficiency, albeit with reduced accuracy.